一、技术背景

键值存储是支撑数据中心和众多数据密集型应用的关键技术,广泛应用于网页检索、电子商务、云存储、社交网络等领域。与关系型数据库不同，键值存储没有关系查询语言，而是通过插入、查询、删除键值对等简单操作来完成数据管理。

在数据密集型应用中，键值存储可以提供更好的写入性能以及相对较快的查询性能。贝格迈思明睿智能数据库作为一款高性能分布式数据库，我们选择LSM-Tree作为存储引擎的基础数据结构，本文是贝格迈思在数据库产品开发过程中，通过对数据库存储过程深层次的实验和分析，对存储基础数据结构的一次探索优化。‌‌

二、键值存储系统的底层数据结构

键值存储系统的核心是实现一个存储键值对的数据结构，要求实现读开销、写开销和存储空间放大三者之间的平衡。常见使用哈希表、B+ Tree和LSM-Tree（Log-Structure-Merge Tree）作为键值存储系统的底层数据结构。

1、哈希表

哈希表能够实现高效的单目标键查询，但是无法进行范围查询，此外哈希表还需要在内存中维护所有键及值指针，内存开销极高。

2、B+树

B+ Tree能够维持稳定的查询开销，但是它是一个就地更新（In Place Update）的数据结构，会造成严重的写放大问题，如Read-Update-Write操作可能会造成大量的脏页写到硬盘中。

3、LSM-树

LSM-Tree是一个非就地更新（Out of Place Update）的数据结构，它首先会将把所有写入缓冲在内存中，当容量达到阈值后再批量的以追加的形式刷到磁盘当中。

LSM-Tree的主要思想是使用了顺序写代替了随机写，提供了高速的写入性能，代价就是略微降低读性能。

与B+ Tree相比，LSM-Tree的数据注入速度更快，写放大效应相对较小，即使查询性能会随着数据存储规模的增大而降低，但在与内存高速索引数据结构（如Bloom-Filter， Fence Pointers， Cache）结合依然可以带来高速读能力。因此在写数据密集的工作负载中，LSM-Tree更加受到开发者和业界的青睐。

从实现上看，LSM-Tree是一种分层有序、基于硬盘的数据存储结构。这里的分层指的是分内存和硬盘的存储，在硬盘上以文件的形式分层存储。基于LSM-Tree的键值存储系统的常见架构如图1所示。

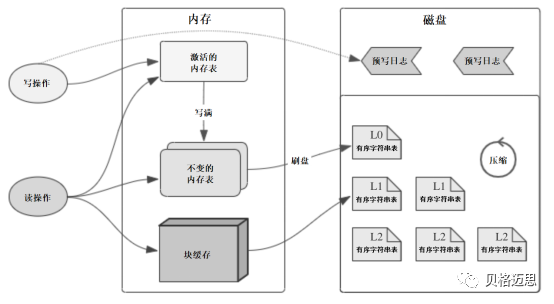
在执行写操作时，首先写入预写日志（Write Ahead Logging， 简称WAL）和激活的内存表（Active MemTable）。因为内存表（Memory Table，简称MemTable）会断电丢失数据，因此需要将记录写入磁盘中的 WAL 保证数据不会丢失，即使崩溃也可以由预写日志将崩溃前的状态恢复出来。

MemTable是一种在内存中的数据结构，它保存了落盘之前的数据。跳表（SkipList）是最流行的 MemTable 实现方式，LevelDB、PebblesDB 和 RocksDB 等流行的键值存储系统均默认使用跳表作为 MemTable。

激活的MemTable写满后会被转换为不变的内存表（Immutable MemTable），并新创建一个空的激活的MemTable。后台线程会将不变的MemTable写入到磁盘中形成一个新的有序字符串表（Sort String Table，简称SSTable）文件，并随后销毁不变的MemTable，并回收其在WAL日志中的空间。

SSTable是LSM-Tree在硬盘中持久化存储的数据结构，是一个有序的键值对文件。LSM-Tree不会修改已存在的SSTable，而是直接在MemTable中写入新版本的数据，并等待MemTable落盘形成新的SSTable。因此，虽然在同一个SSTable中key不会重复，但是不同的SSTable中仍会存在相同的key。

在执行读操作时，由于最新的数据总是先写入MemTable，所以在读取数据时首先要读取MemTable然后从新到旧搜索SSTable，这样可以保证找到的第一个版本就是该key的最新版本。根据局部性原理，刚写入的数据很有可能被马上读取。因此，MemTable在充当写缓存之外也是一个有效的读缓存。

为了提高读取效率SSTable通常配有Bloom-Filter和Fence Pointer来快速判断其中是否不包含某个key以及在包含时快速定位它的位置。因为读取过程中需要查询多个SSTable文件，因此理论上LSM-Tree的读取效率低于使用B+ Tree的数据库。为了提高读取效率，RocksDB中内置了块缓存（Block Cache）将频繁访问磁盘块缓存在内存中，而LevelDB内置了块缓存和表缓存来缓存热点数据块和SSTable。

随着不断的写入SSTable数量会越来越多，数据库持有的文件句柄会越来越多，读取数据时需要搜索的SSTable也会越来越多。另一方面对于某个key而言只有最新版本的数据是有效的，造成了磁盘空间浪费。因此对SSTable进行压缩（Compaction）就十分重要。无论是学术界还是工业界，对于LSM Tree的优化都落在了Compaction操作上。

三、压缩相关重要概念

读放大、写放大和空间放大是跟压缩有关的3个重要概念。

读放大是指读取数据时实际读取的数据量大于真正需要的数据量。例如LSM-Tree读取数据时需要扫描多个SSTable。

写放大是指写入数据时实际写入的数据量大于真正的数据量。例如在LSM-Tree中写入时可能触发压缩操作，导致实际写入的数据量远大于该key的数据量。

空间放大是指数据实际占用的磁盘空间大于实际需要存储的数据量。例如上文提到的SSTable中存储的旧版数据都是无效的。

四、压缩策略介绍

压缩策略需要在三种负面效应之间进行权衡以适配具体应用场景。

1、大小层级压缩策略

大小层级压缩策略（Size Tired Compactaction Strategy，简称STCS）保证每层存储数据的大小从上到下呈指数型增长，同时限制每一层SSTable的数量。当某一层SSTable容量之和达到阈值（通常是与下一层容量大小的比值T）后则将它们合并为一个大的SSTable写入到下一层。

STCS实现简单，缺点是每一层的SST当层数较深时容易出现巨大的SSTable。此外，即使在压缩后同一层的SSTable中仍然可能存在重复的key。这样导致一方面存在较多无效数据即空间放大较严重，另一方面读取时需要从旧到新扫描每一个SSTable，导致读放大严重。与下面介绍的分层压缩策略相比，STCS的写放大较轻一些。

2、分层压缩策略

分层压缩策略（Leveled Compactaction Strategy，简称LCS）也是采用分层的思想，每一层限制总文件的大小，同样是当某一层SSTable容量之和达到阈值后他们将合并后写入到下一层，且保证下一层的SSTable间逻辑上有序。

LCS会将每一层切分成多个大小相近的SSTable，且SSTable在层内是有序的，一个key在每一层至多只有1条记录，不存在冗余记录，因此在逻辑上一层是一个SSTable。

LCS层内不存在冗余所以空间放大比较小。因为层内有序，所以在读取时每一层最多读取一个SSTable，读放大较小。在读取和更改较多的场景下LCS有着显著优势。当某一层的总大小超过阈值之后，LCS会从中选择一个SSTable与下一层中所有和它有交集的SSTable合并，并将合并后的SSTable放在下一层。其中，与每个有交集的SSTable进行合并保证了压缩之后层内仍然是有序且无冗余的。

3、压缩策略的选择

因此压缩策略的选择对键值存储系统的读性能、写性能和空间效率有较大影响。在STCS和LCS之间，控制压缩频率最重要的因素是邻近两层之间大小的比值T=size（Li+1）/size（Li），其中size（Li）表示Li层的文件大小阈值。

在STCS下，当T值增大时，压缩操作的频率降低，最终变成日志的记录方式。在这个最终状态，写放大效应最小，但查询开销高、空间放大问题最为严重。

在LCS下，当T值减少时，压缩操作更加频繁，最终变成有序数组的记录方式。

在这个最终状态，查询操作可以通过栅栏指针在一次读取操作中完成，并且不会读取冗余的键值对，因此读效率高，但写放大问题严重。图2展示了两种压缩策略的权衡状况，其中X轴为更新开销，Y轴为查询开销，曲线是由LSM-Tree选择不同的T值来生成的，两个端点代表日志记录和有序数组记录。

面对多样的应用场景和复杂的数据负载，现有键值存储系统对LSM-Tree的调优往往顾此失彼，且随着数据规模的增长，有可能使曲线向右上方移动，导致系统性能可伸缩性差。

不论采用STCS还是LCS压缩策略，LSM-Tree中压缩操作的频率控制着写开销、读开销以及存储空间之间的权衡。目前存在在图2这条曲线上的设计总是次优的。

五、贝格迈思创新压缩策略

针对当前LSM-Tree存储系统的压缩策略问题，贝格迈思提出了一种新型压缩策略，称为惰性分层压缩策略（Lazy Leveling Compactaction Strategy，简称LLCS）。

惰性分层压缩策略将LSM-Tree分为最底层（Greatest Level）和上层（Up Levels）两部分，并引入两个参数来确定设计空间中最佳的均衡点。

LLCS沿用现有LSM-Tree的Bloom-Filter和Fence Pointers来优化查询，但给最底层的布隆过滤器分配较少的内存，将其重分配给上层（比如上层的20bits Per Key，下层1bit Per Key），以减低上层的假阳性概率，从而降低系统整体的查询开销。

LLCS中引入的两个参数分别是上层中每一层SSTable的数量K和最底层SSTable的数量Z。

1、LLCS与现有压缩策略区别

LLCS与现有压缩策略的区别有两点：

第一点是压缩触发条件不同。

LLCS中针对上层的每一层，当写入最后一个SSTable时触发合并压缩操作，而现有的基于LSM-Tree的键值存储系统一般是当最后一个SSTable写满时才触发合并压缩操作。

第二点是在每一层设置一个活跃的SSTable，在有序合并某一层所有SSTable后再与下层中活跃的SSTable进行有序合并，生成一个新的SSTable，替换下层参与合并的SSTable。

其中每个上层的Li+1层活跃的SSTable是从该层中文件大小不低于K*size（Li）的SSTable集合中挑选的，一般为最后一个SSTable，而最底层活跃的SSTable是从该层中文件大小不低于Z*size（Lk）的SSTable集合中挑选的，其中Lk是上层的最后一层;若下层中没有文件大小不低于对应阈值的SSTable，则有序合并当前层所有SSTable后不再与下层中的SSTable合并，而是像STCS一样直接在下层添加合并后的SSTable。

2、LLCS本质上是一种参数化策略

如图3所示，LLCS将LSM-Tree分为最底层和上层两部分，并引入两个参数来确定设计空间中最佳的均衡点，以适配混合多变的数据负载。

LLCS沿用现有LSM-Tree的布隆过滤器和栅栏指针来优化查询。为了在相同内存开销下降低系统整体的假阳性概率，需要合理分配每一层布隆过滤器的内存大小。由于采用了栅栏指针，每一层探测访问SSTable的I/O开销是相同的，而查询的键很大概率上都在最底层，因此给最底层的布隆过滤器分配较少的内存，将其分配给上层，以减低上层的假阳性概率，这样就可以跳过较多的层次，从而降低系统整体的查询开销。

LLCS中引入的两个参数分别是上层中每一层SSTable的数量K和最底层SSTable的数量Z。

3、设计LLCS的动机

设计LLCS的动机是提供更大的压缩控制灵活性、更好适配变化的数据负载。

与STCS相比，LLCS具有更低的目标键查询开销、短范围查找开销、长范围查找开销和空间放大率，并具有相同的更新开销。

与LCS相比，LLCS降低了整体的更新开销，具有同样的目标键查询开销、长范围查找开销和空间放大率，以及相近的短范围查找开销。

4、LLCS对LSM-Tree设计空间的拓展

LLCS通过设置不同的参数值，可以在不同的合并压缩策略间进行切换，拓展了LSM-Tree的设计空间。

当K和Z减小时，目标键查询开销、短范围查找开销、长范围查找开销和空间放大率将逐步降低，整体的更新开销将逐渐接近LCS的更新开销。

当K和Z增大时，整体的更新开销将逐步降低，但是目标键查询开销、长范围查找开销和空间放大率都快速增长到STCS的水平。

比较合理的状态是K=T-1且Z=1，这时目标键查询开销、长范围查找开销和空间放大率跟LCS大致相同，短范围查找开销也接近LCS，但整体的更新开销跟STCS的一样低。

5、LLCS策略实施方法

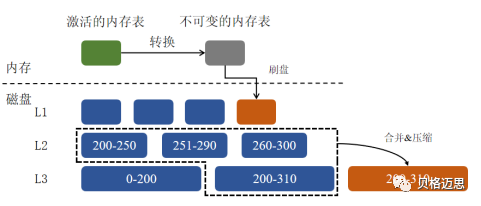
如图4所示，实施LLCS策略时，LSM-Tree上层的SSTable之间是无序的，即存在交叉冗余的情况。当它们的数量达到T时，将它们跟下一层的活跃SSTable合并压缩后刷到下一层;若下一层SSTable的数量达到T，则继续往下递归处理。

六、小结

这篇文章我们简要介绍了键值存储系统及其相关概念。贝格迈思在数据库产品开发过程中，通过对数据库存储过程深层次的实验和分析，创新优化了LSM-Tree作为存储引擎的基础数据结构，进行了存储基础数据结构的一次探索优化。

同时，LLCS压缩策略有着较大的参数空间，许多特性仍然需要更多的实验去验证发现。欢迎各位对贝格迈思持续关注与交流，我们将在未来的技术分享中继续发布更多精彩硬核技术~