一、引言

贝格迈思在自研的高性能智能数据库AiSQL中高效融合了向量数据引擎及向量储存，支持向量的存储、索引，能用于管理来自AIGC场景、深度神经网络或者各类机器学习模型所生成的海量向量数据，高效解决向量相似度检索以及高密度向量聚类等问题。产品具备高可用、高性能、易拓展等特点，支持多种向量搜索索引、数据分区分片、数据持久化、增量数据摄取、向量标量字段过滤混合查询等功能，能够很好满足企业针对海量向量数据的实时查询和检索等需求。

为了提供向量存储和索引功能，AiSQL引入了高效的最近邻近似检索算法HNSW，在分布式存储引擎中实现了HNSW索引和向量数据的管理。

本文重点介绍HNSW算法，从最初的朴素思想构成查询图、NSW（Navigable Small World）的介绍，到经过优化以及引入跳表思想构成HNSW算法的思路，大家来帮助理解这个算法。希望读者读完本文能够对此算法有个较为全面的认识。

二、朴素思想

我们先从朴素查找开始介绍基于图的近似最近邻算法的演进，从下面这张图开始。

1.目的：

假设在一个二维平面中存在这些点集，这些点集的都是二维的向量，我们需要在这个图上根据具体某个查找点进行最近邻查询。

2.方法：

首先需要把某些点与点之间进行关联，构成一个查找图。当查找与粉色点最近的一点时，从任意一个黑点出发，计算当前节点与粉点的距离，并计算黑点的所有邻居点与粉点的距离。如果邻居点距离粉点的最小值小于当前节点与粉点的距离，则认为有邻居点离粉点更近。以距离粉点最近的点作为下一个出发点，并重复以上逻辑，当停止搜索时，则认为当前的点就是离粉点最近的点。

3.具体案例：

查找粉色点最近的邻居点：

1) 从任意一个黑色点出发，比如选C点;计算C点与粉点的距离，同时计算C点的邻居（A，B，I）与粉点的距离。

2) 计算得出，B点与粉点的距离最近，且小于C点与粉点的距离，则把B点作为下一次的查找点。

3） 此时B的邻居节点有（A， C， I， E， H），计算B的所有邻居点到粉点的距离。

4) 计算得出，E点与粉点的距离最近，且小于B点与粉点的距离，则把E点作为下一次的查找点。

5） 此时E的邻居节点有（J，B，D，G），计算E的所有邻居点到粉点的距离。

6) 计算得出，J点与粉点的距离最近，但是大于E点与粉点的距离，说明当前E点已经是与粉点距离最近了，停止搜索，返回E点。

4.这个朴素思想有以下缺点：

1) 有些点没有在连接图上，也即出现没有邻居的点，如K点。

2） 想要找最近的两个点无法做到，即无法返回topN的结果;找到的点可能不是最邻近点。

3) 有些点的邻居点太多，有些可能没必要（减少连接边）。

5. 解决方法：德劳内（Delaunay）三角剖分算法

德劳内三角剖分算法是一种用于解决多边形三角剖分问题的算法，是一种基于贪心算法的算法。它的目标是将多边形分割成最少数量的三角形，以便进行更精确的计算。

此算法相较于朴素思想可达成以下要求：

1) 查找图中每个点都有邻居点。

2) 相近的点之间都是互为邻居点。

3) 图中的所有边的数量最小。

三、NSW算法

NSW（Navigable Small World）全称“可导航小世界”。虽然德劳内三角剖分算法可以很好的解决以上的问题，但NSW（全称"可导航小世界"）算法并没有采用此算法来构建德劳内三角图。原因有两个：构图的算法时间复杂度太高;查找性能较差，如果出发点与查询点距离较远时，需要经过很多次比较，跨越多个邻居点才能到达查询点最近的点。NSW算法引入了"高速公路"的概念，即有些点与较远点有直接通路，在解决朴素思想缺点的同时，相对德劳内三角剖分算法具有更高的查询性能。

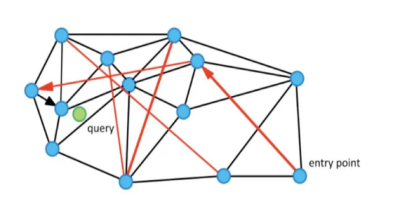
在NSW论文中配了这样一张图，黑色边是近邻点的连线，红色边就是“高速公路”。假设从enter point点进入查找，查找绿色点临近节点的时候，就可以用过红色连线“高速公路”快速靠近到查找点的附近。

1. “高速公路”构成

图中的"高速公路"是如何产生的呢？

先看一下NSW的构图算法：

向图中逐个插入点，当插入一个全新点时，通过朴素思想（即通过计算邻居点和待插入点的距离得出新的进入点）。查找到与这个全新点最近的m个点（m由用户设置），连接全新点到这m个点的连线。

从以上的构图描述中比较难看出"高速公路"形成的过程，可以从简单的NSW构图案例来帮助我们了解形成的过程。

假设要构建一张图，m=3，红色的点代表新插入的点，黑色的代表图中已有的点。每一个新插入的红色点，都会去跟距离红色点最近的m个黑色点建立连接。

Step1：当前无黑点，直接插入。

Step2：当前只有一个黑点为候选点，直接相连。

Step3：当前只有两个黑点为候选点，小于m值，也是直接相连。

Step4：当前刚好有三个黑点为候选点，也是直接相连。

Step5：当前有四个黑点为候选点，则需要在这四个点中选择距离插入点最近的3个相连。

Step6：同step5。

"高速公路"的构成：不难发现，在刚开始构图的时候，对于一个新插入的点，在寻找图中已有的点跟它建立连接的时候，它的候选邻居点很少，因为图才刚开始构建。比如图中Step3，新插入的红点跟已有的两个黑点距离其实很远，但是它们还是建立了连接。而在构图的后期，图中的节点越来越多时，新插入一个点的时候，找到的邻居点确实是比较近的m个节点。因此"高速公路"在构图的早期已经被建立起来了，后期就不太可能会去修改这个高速公路了。

2.查询m个邻居点

NSW又是如何为新插入的点找到m个邻居点的呢？

还是通过具体的案例来理解这个查找的过程，在这个查找过程中会使用到3个队列：

Result队列：存放最终的结果邻居点，size为m，这些点距离新插入点的距离从远到近排序。

Candidate队列：探索过程中的点，这些点距离新插入点的距离由近到远排序。

Visited队列：己经被访问过的点，减少重复查询。

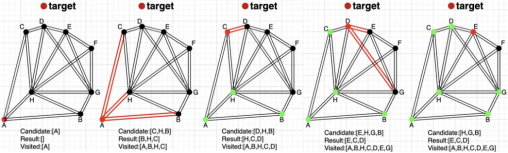
选择A作为起始点，绿色代表已经访问过的点，红色点代表当前探索队列中距离target最近的点；此时A 的邻居点作为候选点Candidate:[C,H,B]，结果队列Result:[B,H,C]，被访问过的则是Visited:[A,B,H,C]。

继续从候选点中取最近的一个点C，再把C的邻居点D放入到候选队列中Candidate:[D,H,B]；D点离target距离比结果队列Result:[B,H,C]最远的点B的距离小，把B从结果队列中去掉（因为m=3），同时把D放入到Visited队列中。

最后一个图中，候选队列中Candidate:[H,G,B]距离target最近的是H点。H点与target之间的距离已经大于或等于结果队列中Result:[E,C,D]距离target最远的距离了，所以此时搜索完成，返回Result队列。

因此当需要新插入target这个点时，找到的3个最近邻居点为[E,C,D]。

四、HNSW算法

Hierarchical NSW全称“分层可导航小世界”，是NSW算法之上的更进一步的优化版本。其核心思路就是在NSW算法的基础上引入跳表来实现分层的思路，从而进一步优化到目标向量的检索速度。即是使用多个小世界（层次结构）+概率分布+图遍历来近似最近邻搜索。

1.先来认识另一个数据结构：跳表

简单有序的单链表，如果要查找某一个数据，只能从头开始遍历，直到找到相应的点返回。但这样的查询效率很低，时间复杂度是O(n)级别。假如对有序单链表进行改造，增加多层有序索引的链表，如下图，则有三个层次的索引链表。

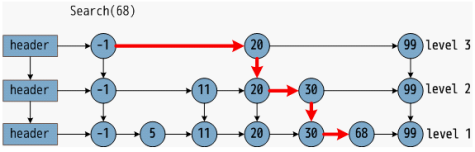
1.1查找算法如下：

从顶层开始查找移动到当前节点的右指针指向的节点，直到右节点的key值大于要查找的key值时停止；如果还有更低层次的链表，则移动到当前节点的下一层节点，如果已经处于最底层，则退出；重复第2步 和 第3步，直到查找到key值所在的节点，或者不存在而退出查询。

来看一下具体案例：

1） 如需要查找68这个结点，从最顶层（level 1）结点找到20，下一结点是99，则停止本层（level 1）查询。

2） 移动到下一层（level 2）结点20，移动到右指针指向的节点30，因为下一结点是99，停止本层（level 2）查询。

3） 移动到下一层（level 3）结点30，移动到右指针指向的节点68，找到结点，返回。

跳表的查询因为有了上层的"高速公路"，能够减少比较次数快速找到相应的结点。

1.2跳表的构建

通过抛硬币的方式决定新插入的结点是否插入到上一层索引链表中，如果为正面，则在上一层插入此新结点；继续抛硬币，如果为正面，重复前面的步骤，直到最顶层；如果为反面，则不再往上一层插入。

如插入30这个结点，在level 1时插入后，抛硬币决定是否往level 2层插入，当为正面时，则在level 2插入此结点;然后在level 2层继续抛硬币决定是否往level 3层插入结点，直到最顶层，或者为反面时终止插入过程。

2.HNSW思想

引入跳表思想，把NSW图存成看作是有序链表，然后构建成多层级的连接图。

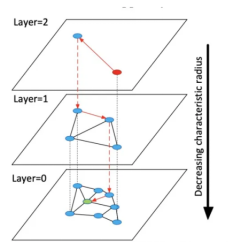
第0层中，是数据集中的所有点，根据上图查找绿色点的最近邻点。从表层（上图中编号为Layer=2）任意点开始查找，经过三层就能够快速找到查找点的最近邻居点。

2.1执行查询流程举例：

为便于理解，假设有这一组二维的向量如下图，在一个二维的平面中，指定某一个点，找到在这个二维平面中最近的5个邻居：

如果使用暴力方法的话，则遍历每一个点，计算每一个点到指定点的距离，并把结果进行排序，得到最近的5个邻居。但是这个方法在大规模数据集上是不可行的，也是最昂贵的做法。

Step1：根据HNSW思想，先创建一个只有12的点稀疏点集。

Step2：然后添加另外一个图层，将这12个点映射到更加密集的图层上。

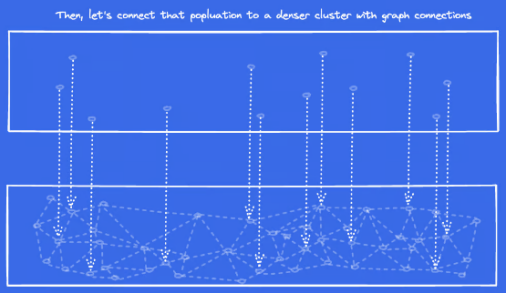
从上图的顶层，取10个与指定点距离最近的点，然后将箭头指向底层的10个点作为候选点，遍历这10点的所有邻居，比较距离最后只保留10个最接近的列表，其他不保留（这个10即后面要介绍的参数ef）。

Step3：继续添加另外一个图层，再做同样的一个事情。

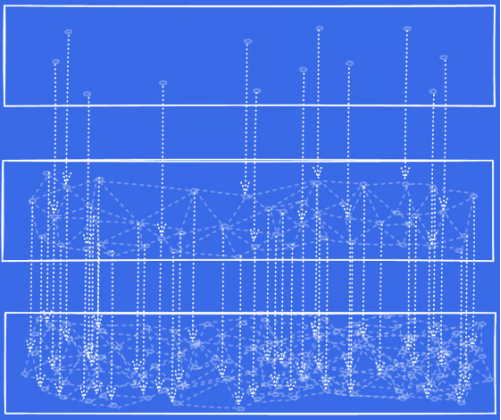
Step4：用上面得到的10个点导航到更密集层的点，同样遍历它们的连接点，计算出前10的列表，最后返回5个结果。

可以看到"分层可导航小世界"这个名字的来源，这是一个层次结构。因为数据是越来越密集的，这个图是可以导航的，可以从稀疏移动到密集。

2.2在HNSW算法相关论文中有提供以下5个主要算法：

1） INSERT（hnsw，q，M，Mmax，efConstruction，mL） ： 新元素 q 插入算法。

2） SEARCH-LAYER（q，ep，ef，lc） ： 在第 lc 层查找距离 q 最近邻的 ef 个元素。

3） SELECT-NEIGHBORS-SIMPLE（q，C，M） ： 在候选点集合 C 中 选取距离 q 最近邻的 M 个元素。

4） SELECT-NEIGHBORS-HEURISTIC（q，C，M，lc，extendCandidates，keepPrunedConnections） ： 探索式寻找最近邻。在插入中使用。

5） KNN-SEARCH（hnsw，q，K，ef） ： 在 hnsw 索引中查询距离 q 最近邻的 K 个元素。

很明显，构建多层次结构的连接图，对于查询性能是有很大的改善，但同时也增加的资源的消耗。即通过空间换时间来达到一定的平衡。

到此为止，我们可以对于HNSW的优化演进过程有了基本了解。

3.HNSW索引的使用：

1） 构建HNSW索引的方法：

使用 HNSW（vector_col vector_l2_ops） 和 （M=4， ef_construction=10） 在表上创建索引。

2) 支持三种距离度量方法：欧氏距离、内积、余弦距离，对应的创建索引方法如下：

使用 HNSW（vector_col vector_l2_ops） 在表 上创建索引 （M=4， ef_construction=10）;

使用 HNSW（vector_col vector_ip_ops） 在表 上创建索引 （M=4， ef_construction=10）;

使用 HNSW（vector_col vector_cosine_ops） 在表 上创建索引 （M=4， ef_construction=10）。

3） 同时也提供了三种距离的操作符支持SQL查询

选择 id， vector_col， vector_col<-> '[2， 3， 3]' 作为与test_vector订单的距离 vector_col<-> '[2， 3， 3]“;

选择 id， vector_col， vector_col<#> '[2， 3， 3]' 作为与test_vector订单的距离 vector_col<#> '[2， 3， 3]“;

选择 id， vector_col， vector_col<=> '[2， 3， 3]' 作为与test_vector顺序的距离 vector_col<=> '[2， 3， 3]'。

4) 此索引有如下特点：

结果是近似值，与其他向量索引类型没有区别；

比基于列表的索引有更好的性能；

需要更长的索引构建时间；

需要更多的内存资源。

4.构建参数说明

构建索引需要遍历数据表中所有值，当循环到下一个值时，利用之前构建的索引与算法将值插入到图中。即每个点都需要放在它所到达层以下的所有层中，并且每个点都需要连接到它能找到的最近的点。在大规模的数据集上，则需要通过一些参数来限制构建的过程。

1） m：

m是索引中每层每个点与最近邻接点的连接数(默认是16)，范围[2,100]。通过这个参数，创建索引时限制了该层各点之间的连接数量。构建时间随着m值的减小而减小，根据测试，m的合理取值范围是5到48。测试结果对于低召回率和/或者低维数据，较小的m通常产生更好的结果。而对于高召回率和/或者高维数据，较大的m更好。

2） ef_construction：

ef_construction是索引构建期间使用的候选列表大小（默认是40），范围在[4,1000]。上面的查询执行案例中，保留10个候选结果就是对应这个字段的值。在索引构造期间，每一条数据库表记录的值都需要放入索引结构中，后来的记录使用当前构建的索引。在索引构建过程在图层之间移动时，会保留上一层最接近的值的列表，列表大小则由此字段控制。ef_construction的值越大，索引构建越慢。也即是构建速度与索引质量可以通过此参数进行调整。增加这个值不会带来性能上的提升，可以提高准确率，但换来更多的构建时间。ef_construction和m之间的关系是ef_construction需要大于等于m值的2倍。

3） 查询时参数ef_search：

ef_search用于限制列表中维护的最近邻居的数量（默认值是40）范围[1,1000]，较小的ef_search值将有更快的查询，但有不准确的风险。设置方式：SET hnsw.ef_search = 5。

五、结语

本篇文章分享了HNSW算法逐步演进的过程，可以清晰理解HNSW算法的底层基础。AiSQL中提供了HNSW在分布式数据库中的适配实现，能够满足用户对大规模高维向量数据管理和处理的需求，为开发者提供了简单易用的API接口和工具，方便地集成和应用于各种应用场景。AiSQL中基于HNSW算法的向量数据引擎可用于处理具有复杂的特征表示和相似性度量的数据，如图像、音频、文本、生物信息和推荐系统等领域。