一、技术背景

贝格迈思自主研发的高性能智能数据库AiSQL系统BigInsights，融合了向量数据引擎与向量储存，支持向量数据存储、索引和检索，可用于管理和分析来自AIGC场景、深度神经网络及各类机器学习模型所生成的海量向量数据。BigInsights充分运用了原生混合检索算法（即NHQ算法），高效解决了大规模向量数据的结构化和非结构化的混合查询情景下性能不佳的问题，并不断通过多种混合索引的核心算法和策略进行优化，为大规模非结构化数据的应用体验保驾护航。

本文将重点介绍BigInsights采用的混合检索(NHQ)技术方案。首先，总结和介绍了现有不同混合检索(HQ)策略及问题；其次，阐述了新的混合检索(NHQ)技术方案；最后，进一步描述了NHQ的技术实现方法。

关键词释义：

PG: proximity graph近邻图

PGs：proximity graphs近邻图集

HQ：（hybrid query）混合查询

NHQ：（Native Hybrid Query）原生混合查询

ANNS:（approximate nearest neighbor search）最近邻相似性搜索算法。

二、向量数据的重要作用

我们知道，向量数据库Vector Database在构建基于大语言模型LLM的行业智能应用中扮演着重要角色。向量数据库存储和处理向量数据，提供高效的相似度检索功能。通过向量嵌入（Vector Embedding），将企业知识库文档和数据转化为向量表示，并与大模型进行交互，实现专有或私域的垂直行业智能化应用。

基于大语言模型构建行业智能应用为什么需要向量数据库？

“ Vector 是模型之根，是大模型与知识库交互之桥”，向量嵌入（Vector Embedding）是一种AI原生的数据表示方式，适用于各种基于AI的工具和算法。它可以表示非结构化的数据及知识，如文本、图像、音频和视频等。

关于向量嵌入，罗伊·凯恩斯（Roy Keynes）的定义是：“嵌入（vector embedding）是学习的转换，使数据更有用”。神经网络深度学习将文本转化为一个包含实际含义的向量空间。这更有用，因为它可以找到同义词，以及单词之间的句法和语义关系。最为经典的例子：Queen=King-Man+Woman。

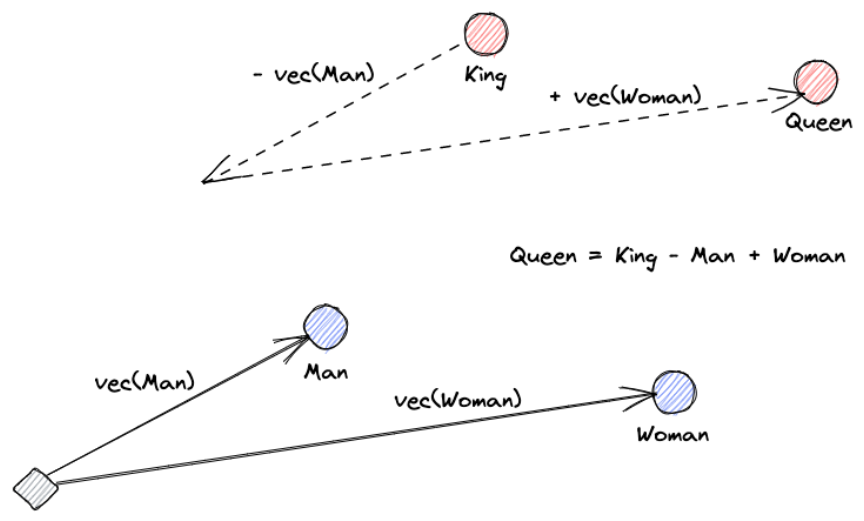
在我们了解认识到向量嵌入的原理之后，向量数据库是怎么工作的呢？

向量数据库的工作方式是使用算法对向量嵌入建立索引和进行查询的。这些算法通过哈希、量化或基于图表的搜索来实现近似最近邻 (ANN) 搜索。为了检索信息，ANN 搜索会找到查询的最近邻向量。与 KNN 搜索（已知最近邻，或真正的 k 最近邻算法）相比，ANN近似最近邻搜索的计算量较小，准确性也较低，但它适用于高效、大规模地处理高维向量的大型数据集。

向量数据库流程类似于下图所示：

1.索引：使用哈希、量化或基于图表的技术，向量数据库通过将向量映射到给定的数据结构为向量建立索引。这样可以实现更快的搜索速度。

① 基于哈希：哈希算法（例如局部敏感哈希 (LSH) 算法）是一种用于高效近似最近邻搜索的技术。可以理解为一种具有特定性质的hash function，用于将海量高维数据的近似最近邻快速查找，而近似查找便是比较数据点之间的距离或者相似度，其最大特点就在于保持数据的相似性。它在大规模数据集中寻找相似项，例如在图像、文本或其他数据类型中找到相似的对象。

② 基于量化：量化技术（例如乘积量化 (PQ：Product quantization)）会将向量分解成较小的部分，并用代码表示这些部分，然后将这些部分重新组合在一起。结果是一个向量及其分量的代码表示。这些代码的集合称为码本。当被查询时，使用量化的向量数据库会将查询分解为代码，然后将其与码本进行匹配，以找到最相似的代码来生成结果。

③  基于图表：图表算法（例如分层可导航小世界 (HNSW) 算法）使用节点来表示向量。它会对节点进行聚类，并在相似节点之间绘制线或边，从而创建分层图表。启动查询后，这种算法会在图表层次结构中导览，以找到包含与查询向量最相似的向量节点。

2.查询：当向量数据库接收到查询时，它会将索引向量与查询向量进行比较，以确定最近邻向量。为了建立最近邻，向量数据库依赖的是称为相似度度量的数学方法。目前有不同类型的相似度度量方法：余弦相似度，欧式距离等。

① 余弦相似度建立的相似度范围在 -1 到 1 之间。通过测量向量空间中两个向量之间的夹角余弦，它可以确定向量是截然相反（用 -1 表示）、正交（用 0 表示），还是相同（用 1 表示）。

② 欧氏距离通过测量向量之间的直线距离来确定 0 到无穷大范围内的相似度。完全相同的向量用 0 表示，数值越大，表示向量之间的差异越大。

三、为什么需要混合检索

向量数据库大多数的通用场景，给定一组对象（例如一组图像）和一个查询对象，我们可以很容易地将每个对象转换为特征向量，并应用向量相似性搜索来检索最相似的对象。但是实际生产环境中，经常会遇到一些结构化数据与非结构化数据需要同时检索的场景。

而现有的HQ（混合查询）的解决方案是在“分解-组装”模型中设计的，其中HQ被分解为两个子查询：ANNS基于向量索引，AF基于属性索引。

目前关于这两个子查询的执行顺序有两种实现策略，如下图的策略A和策略B。

我们先看一个传统HQ算法应用的场景：

假设有一个带条件的拍图查找商品需求：查找与输入图片相似度最高，价格在100到200元之间，并且上架时间在最近一个月以内的前100件商品。

应对这种场景，业界现有的一些方案支持主要分为三类：

第一类：暴力查询

根据结构化条件获取所有符合条件的行，再在其中根据向量距离进行排序，选择距离最小的100条数据进行输出。这种执行计划召回为100%，但是查询速度最慢，在底库过大或符合结构化条件行数过多时查询性能低下。

第二类：纯向量查询 + 结构化过滤

为了加速查询，先使用向量索引查询出与输入图片最接近的N行数据，再在其中根据结构化条件进行过滤。这种执行计划的优点是查询速度最快，缺点是如果结构化查询的筛选率太小（即一行数据通过过滤的概率太小），则查询最终输出的数据行数可能比用户要求的行数少。

第三类：向量结构化混合检索

向量结构化混合查询结合了第一类和第二类执行计划，既能使用索引，又能解决第二类执行计划返回数据变少的问题。同时，如果结构化条件列上有索引，且索引类型支持Bitmap（左子树）生成，则混合查询还可以利用其他索引来生成Bitmap，从而进一步加速混合查询。

现存的业界已经实现的混合查询应用：

Vearch（京东）该策略很容易扩展到其他专用的向量相似度搜索库，如SPTAG,NGT,Faiss。

阿里的ADVB,基于乘积量化（PQ）添加了多个查询计划，面对场景3，阿里的解决方案计划大致如下图所示：

Milvus按照访问频繁程度划分子集，这样可以更快的搜索到符合查询的子集，然后对子集进行向量相似度搜索。

这些确实解决了混合检索的问题，但是做的还不够好。这些的解决方案都是在用”分解-组装“的模型来响应混合索引，但都存在不是很友好的问题，需要优雅解决。具体如下：

1.必须同时维护两个索引（属性索引、向量索引），这不仅增加了内存开销，而且它还引入了额外的逻辑和一个后处理步骤（合并的过程），以确保两个索引的一致性和查询结果的正确性。当数据变化经常变化时，很难同时更新不同的索引。

2.由两种独立的修剪策略造成的不必要的计算开销。

3.查询结果依赖于两个子查询系统候选结果（C1、C2）的合并，但是最后的结果是远远少于期望结果（C1∩C2 << K），这是因为现有的方法分别进行ANNS和AF，所以每个系统只能返回一种约束类型的对象，为了使和合并的结果更大，我们需要是让两个子查询系统C1和C2更大，这样使两个系统都会更加耗时。

4.现有的解决方案对PGs（邻近图）并不友好，比如ADBV和Milvus，他们只对ANNS使用PQ，但是PG比PQ快10倍。

因此我们需要找到一种方法在HQ（hybrid query）中使用PGs。一种简单的办法是将基于PQ的向量索引替换为基于PG的向量索引，但会存在一些问题。在先AF(attribute filtering)后ANNS的策略中，我们希望从经过属性过滤的向量的动态空间中找到相似的向量，在运行时为这些过滤的向量构建向量索引效率会很低，也会占用更多内存空间。

总之，大多数这些局限性的原因是因为这些方法都是在用”分解-组装“的模型来响应HQ，HQ被分为两个子查询，分别处理，然后组合结果。那么，有没有一种新的混合查询框架，适合现有的PGs，提供设计良好的混合索引和联合剪枝模块，以支持非结构化和结构化的查询约束，而不是同时维护两个独立的索引和剪枝操作呢？

四、一种新的混合检索技术方案-NHQ

前面我们已经描述了传统已有的方案中存在一系列问题：

1. 维护两个索引的问题。

2.两种单独剪枝开销大的问题。

3.候选结果合并的问题。

那具体是如何去解决的呢？

我们的解决方案是通过使用一种新的融合策略，如下图所示：

它具备以下特点：

1.无需维护两个索引

带有属性约束的ANNS的NHQ，使用Feature vector + Attribute constraints 以融合的方式组成混合索引。

2.无需两种单独剪枝，解决开销大的问题

综合考虑特征向量和属性约束对混合索引上的搜索空间进行剪枝。

3.无需合并候选结果

它将会直接获得最后的top-k的结果，而并不需要合并操作。同时，它还是一个通用的框架，其中的混合索引是基于PGs的，因此，它与PGs可以很好的融合，而且支持自定义优化的PGs。

4.1揭开NHQ的技术面纱

在介绍NHQ之前，先介绍一下PG(proximity graph)。

PG的定义：
 给定一个对象集S，我们定义S的PG(a距离阈值B)为一个图G=(V,E)，它具有顶点集V和边集E；

1. 对于每个顶点u∈V,它都对应一个对象E属于E属于S。

2. 对于V的任意两个顶点ui和uj，如果ui uj ∈ E，我们有 δ(ν(ui)，ν(uj)) ≤ B，ν(ui) 和 ν(uj) 分别是物体 ui 和 uj 的特征向量。

了解了PG的定义之后，我们设 N(ui)为 ui 的邻居集。我们的想法是构建一个同时使用特征向量和属性作为复合索引的PG，在这个索引当中，u的邻居可能具有和u相同的属性。我们可以用公式1来衡量特征向量之间的距离。

但我们需要量化属性并定义一个距离度量函数。然后，将特征向量距离和属性距离融合为融合距离，对目标进行比较。因此，我们可以直接根据融合距离对特征向量不同或属性不同的顶点进行剪枝。

实现的整体框架，可参见下图：

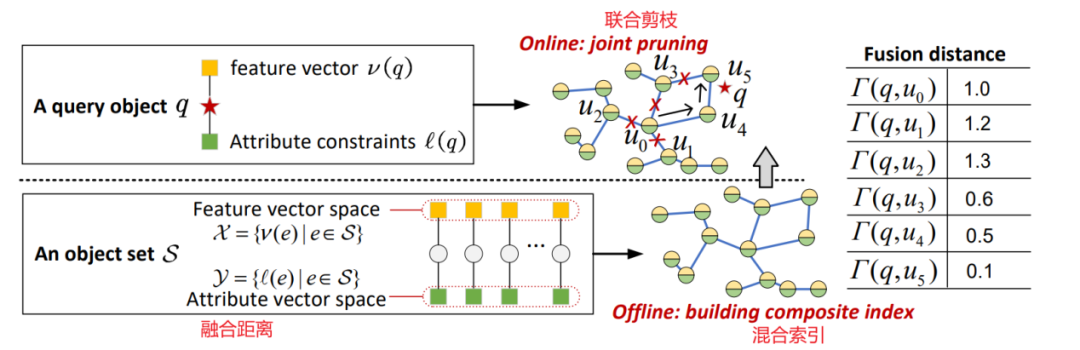
NHQ框架由几个核心算法组件组成：融合距离，权重配置，混合索引，联合剪枝。其中也包含了提高ANNS整体性能的可导航PG，选边策略，路由策略等。

具体算法详细描述见以下各节。

4.1.1融合距离

给定一个特征向量为X的对象集 S，我们可以使用不同的编码方法对每个属于 S 的对象 e 的属性进行编码。顺序编码对于结构化属性的效果很好。我们使用顺序编码 e(.) 来对每个对象 e 得到一个属性向量 l(e) = [l(e)^0，……，l(e)^(m-1)]，其中 l(e)^i 为 e.ai's 的编码值（例如：{NeurIPS, NLP} 可以用 l(.) 编码为[1,3]）。

然后，我们得到属性向量 Y = {l(e)|e∈S}。我们可以使用公式1来测量 X 中两个特征向量 v(ei) 和 v(ej) 之间的距离，用公式2、3测量 Y 中两个属性向量 l(ei) 和 l(ej) 之间的距离。该距离越小，则属性向量越相似。

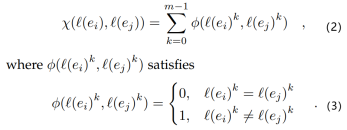
其中，m 表示 l(ei) 的维数，k 表示 l(ei)^k 是第 k 维上的值。我们可以通过使用公式4将特征向量距离 δ(v(ei),v(ej)) 和属性向量距离 X(l(ei)， l(ej)) 融合为对象 ei 和 ej 的单个距离 Г(ei,ej)。

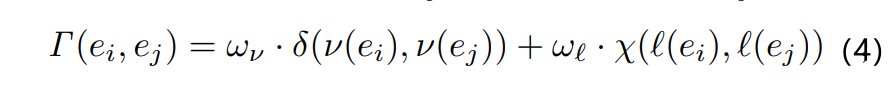
其中 wv 和 wl 是距离权值。

这个距离越小，物体在特征向量和属性上越相似。公式4是一个简单实用的结合两个不同距离的方法。这也使得在现有 PG 之上构建复合索引变得容易，因为我们只需要将距离度量从公式1变为公式4。

例如，如果我们设置 wv=1，wl=0，我们可以得到 Г(ei,ej) = X(l(ei),l(ej))，这与基于特征向量构建 PG 得到的结果相同。设 wv = 0，wl = 1，可以得到 Г(ei,ej) = X(l(ei),l(ej))，与基于属性构造的 PG 相同。由此可见，我们可以通过调整 wv 和 wl 来找到两个距离之间的最佳平衡点

4.1.2权重配置

wv = 1 和 wl = δ(v(ei),v(ej))/m对于大多数数据集和算法给出了最好的查询性能。这些权重不依赖于数据集，只依赖于两个对象的特征向量距离 δ(v(ei),v(ej)) 和属性向量维度 m。其思想是用属性距离微调特征向量距离。

例如，如果 ei 和 ej 具有相同的属性，即 X(l(ei),l(ej))=0，我们保持特征向量距离不变(即 Г(ei,ej) =δ(v(ei),v(ej)))。如果 ei和ej 有完全不同的属性，即 X(l(ei),l(ej))= m，我们将特征向量距离加倍得到 Г(ei,ej) = 2·δ(v(ei),v(ej))。一般来说，我们有 δ(v(ei), v(ej)) ≤ Γ(ei, ej) ≤ 2·δ(v(ei),v(ej))。

4.1.3混合索引

对于图 G = (V, E)，我们令 V = S，此时每个对象 e ∈ S 都是 G 中的顶点 u ∈ V 且 E 为空集。如果 Г(ui, ui) ≤ B'，就在 ui 和 uj 两个顶点之间添加一条边 ui,uj ∈ E，，其中 B' 为融合距离的阈值。值得注意的是，复合索引的融合距离范围极小，不会产生额外的空间成本。

4.1.4联合剪枝

给定一个查询对象 q，我们使用一个复合索引 G 和一个种子集 P（通常从 V 中随机选取）来寻找 top-k 的近似对象。我们遵循以下步骤(见图 6，右上方)

1.初始化。使用访问顶点集 C 来存储搜索扩展的顶点，使用大小为 k 的结果集 R 来存储当前查询结果。最初先把两个集合都设为 P。

2.搜索扩展。我们从 C 中把最小的顶点 ui ∈ Γ(q, ui) 提出来作为下一个访问的顶点，然后添加 N(ui) 到 C 中。

3.查询结果更新。我们用 N(ui) 中更好的顶点来更新 R。对于任意顶点 uj ∈ N(ui) 和一个离 q 最远的顶点 ur ∈ R，如果 Γ(q, uj) < Γ(q, ur)，这意味着 uj 在特征向量和属性上都比 ur 更接近 q，我们就用 uj 替换 ur。

重复2、3步骤，直到 R 不变，然后返回 R 作为 top-k 的近似对象。

4.1.5可导航PG

为了形成混合索引，可以在 NHQ 中部署一个特定的 PG，并将其原来的距离度量更改为公式4的融合距离。这使 PG 能够有效地处理 属性约束ANNS。然而，目前基于 PG 的综合指标存在一定的局限性，影响了 NHQ 的性能。因此，作者分别对边选择和路由策略进行了优化，设计了两款新的可导航 PG(NPG)，以实现在 PG 上的构建和搜索。

4.1.6选边策略

边的选择是构建PG索引的关键步骤，它决定了对象集 S 中每个对象 e 的邻居。不同的策略为对象集构建了不同的结构，这影响了对象集的搜索性能。现有的 PG 根据两个因素进行边选择：

D1：两个顶点之间的距离；

D2：所有顶点的分布。

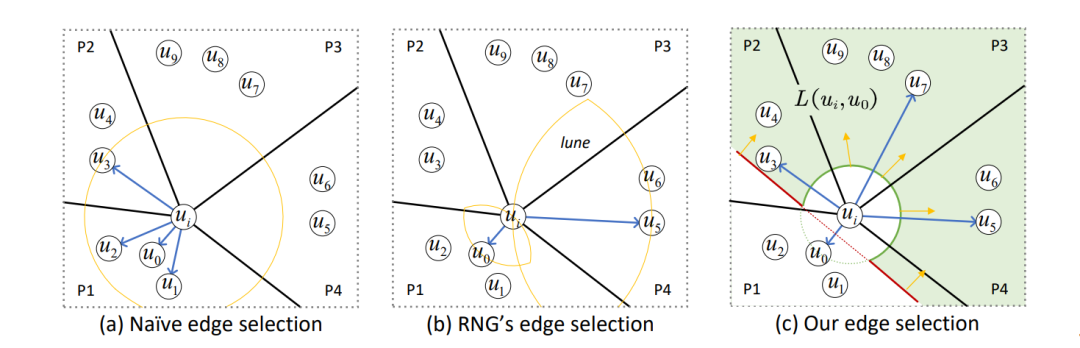
早期的 PG，如 NSW 和 KGraph 只使用 D1，并将每个顶点与其最近的邻居连接(图7(a))。但这会引起冗余计算，降低搜索效率。最近的 PG 也使用 D2 和 RNG 的边缘选择，使邻居的方向多样化。然而，RNG 的边缘选择仍然未能很好地实现邻居的多元化(图7(b))。

我们设计了一种新的利用 D1 和 D2 的边选择策略。它连接 ui 所在每个区域中的一个最近的邻居(图7(c)中的 P1-P4)。

我们定义了着陆区的概念：顶点 ui 及其邻居 uj ∈ N(ui) 的着陆区 L(ui,uj) 是由 H(ui,uj) \ B(ui,δ(v(ui)， v(uj))) 定义的区域。这里，H(ui, uj) 是有 ui 的半空间，它被 ui 和 uj 之间连线的垂直平分线 U(ui,uj) 分割。B(ui,δ(v(ui),v(uj))) 是以 ui 为中心半径为 δ(v(ui),v(uj)) 的超球。

如图7(c)所示，在二维空间中，U(ui,u0) 是连接 ui 和 u0 (即红线)的垂直平分线，H(ui,u0) 位于 U(ui, u0) 的上方，B(ui,δ(v(ui),ν(u0))) 是绿圈包围的区域。因此，由 ui 和 u0 组成的着陆区 L(ui,u0) 为绿色阴影区域（即 H(ui,u0) \ B(ui,δ(v(ui),ν(u0)))）。

为了找到 ui 没有任何邻居的区域，我们将其所有现有邻居的着陆区域相交(即 uj ∈ N(ui) ∩ L(ui,uj))。然后，我们将该区域内最近的顶点添加到 N(ui) 中，使邻居更加多样化。我们的策略确保 ui 的邻居在 C(ui) 所在的区域是多样化的。这是因为我们每次从不同的区域选取邻居添加到 N(ui)。

我们通过以下步骤得到顶点集 V 中的每个顶点 ui的邻居：

1.候选邻居集获取。我们从 (V\{ui}) 中得到 ui 的 l 个候选邻居的集合，用 C(ui) 表示。我们可以使用随机抽样或一个额外的索引来得到 C(ui) (例如，我们基于 NSW 和 KGraph 得到 C(ui))。需要保证 l ≥ R，其中 R 是 ui 的最大邻居数(即 |N(ui)| < R)。

2.邻居初始化。我们按照到 ui 的距离升序对 C(ui) 中的元素进行排序。我们将 N(ui) 初始化为 ui 在 C(ui) 中的最近候选邻居 ut，并将 ut 从 C(ui) 中移除。

3.邻居更新。我们从 C(ui) 中选择距离 ui 最近的顶点，如果它在 ui 和它现有的邻居形成的着陆区 (即 uj ∈ N(ui) ∩ L(ui,uj))，则将其添加到 N(ui) 中。

我们重复这个过程，直到 C(ui) = 0 或 |N(ui)| = R。取得 C(ui) 该过程的时间复杂度取决于使用的方法，忽略获取C(ui)的时间复杂度，在顶点集 V 上选择边的时间复杂度为 O(l·(R + log(l))·|V |)。

4.1.7路由策略

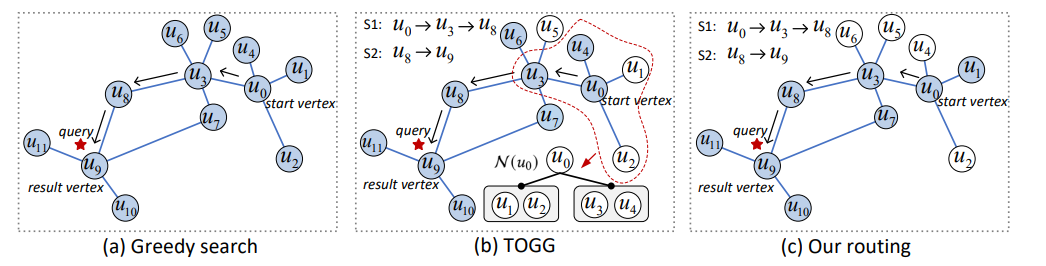
路由是在 PG 上进行搜索的一个关键过程，它确定了从开始顶点到匹配查询的结果顶点的路径。不同的路由策略对搜索的效率和准确性都有不同程度的影响。如图8中的几个策略展示了不同的路由算法：

(a)是贪心算法搜索的路径选择。

(b)是TOGG(两阶段路由策略),TOGG使用了树索引（e.g KD-tree）组织每个节点的邻居。

(c)是当前最新的路由策略算法。

根据距离查询对象的距离将路由分为两个阶段:

S1：远阶段；S2：近阶段。

在本文中采用了随机两阶段路由策略。在 S1 中，我们从 N(ui)随机选择h个邻居(其中 1≤h≤R,R 为最大出度)计算它们到查询对象 q 的距离。这使我们能够快速接近 q 的邻域。在 S2 中，我们遵循类似于贪婪搜索的方法计算 N(ui) 中的邻居到 q 的距离。当 S1 达到一个局部最优值时，就会发生从 S1 到 S2 的转变，即不再更新结果集 R。在 S2 中，我们通过检查访问过的顶点的所有邻居来继续更新 R。当 R 不再接收到任何更新时，搜索终止。

在 S1 中的随机策略并不会降低精度，因为大多数情况下距离查询较远时不需要计算访问顶点的所有邻居到查询的距离，并且可以在 S2 中恢复少量可能丢失的顶点。

我们使用 l1 还有 l2 分别表示 S1 和 S2 中的平均路径长度，路由的时间复杂度为 O((R/h)·l1+ R·l2)。

4.2实验结果

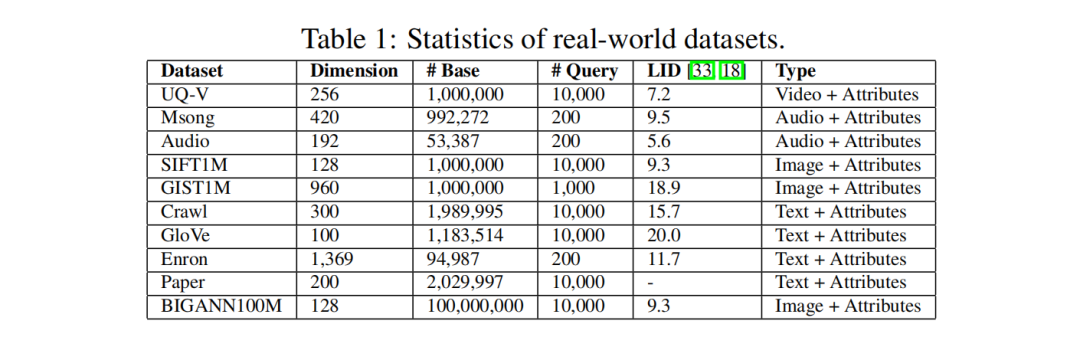
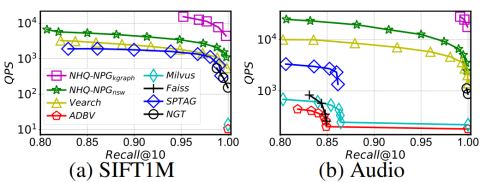
实验使用C++代码，在g++6.5 编译器下进行编译，所有实验配备Intel(R) Xeon(R) Gold 6248R CPU (3.00) GHz) 和755G内存的Linux服务器上进行，使用64个线程构建所有索引，而在搜索过程中只使用一个线程，这是相关工作中常见的设置。本研究使用了十个真实世界数据集，包括视频、图像、音频和文本等各种模态。这些数据集在表1中有详细的特征总结。所有实验报告了三次试验的平均结果。

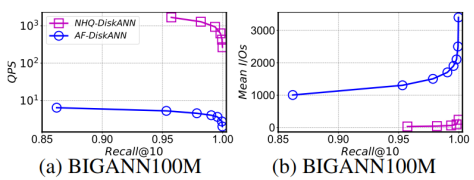
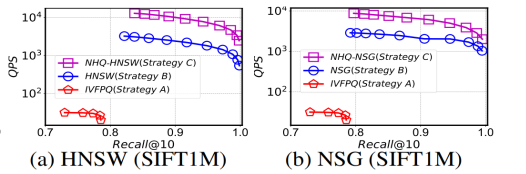
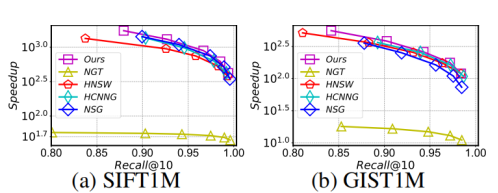
结果显示，在所有数据集上，该方法在 QPS 与 Recall 之间的权衡方面与现有方法相当。例如，当 Recall@10 > 0.99时，NHQ-NPGkgraph 的 QPS 比其他方法高出两到三个数量级。NHQ-DiskANN 在内存和磁盘版本上都优于 Filtered-DiskANN。NHQ-NPGkgraph 在更难的 GloVe 数据集上需要特别其他方法。

五、小结

本文主要阐述了基于PGs(邻近图集)的一种混合查询方案。从复合索引的构建、联合剪枝、选边策略，路由策略等几个方面进行了重点描述。

贝格迈思自主研发的产品明睿智能数据库AiSQL系统BigInsights，通过多种算法的优化实践，充分实现了数据的向量化储存及向量引擎检索。作为数据智能技术创新引领者，凭借业内领先的各项技术，持续开发多种创新型应用产品，打造数据应用生态。

欢迎大家的持续关注，我们期待与大家不断进行技术交流与经验分享，为大家呈现更多精彩纷呈的硬核技术内容。

参考文献

1. Mengzhao Wang, Lingwei Lv, Xiaoliang Xu, Yuxiang Wang, Qiang Yue and Jiongkang Ni.An Efficient and Robust Framework for Approximate Nearest Neighbor Search with Attribute Constraint: 4 - 7.

2. A Implementation Strategy Analysis for HQ: 1, 4, 9.